1. Графы. Основные понятия и определения. Матрицы смежностей вершин графов. Матрицы инциденций графов и орграфов. Степени вершин и полустепени исхода и захода. Основные типы графов.

Основные понятия и определения.

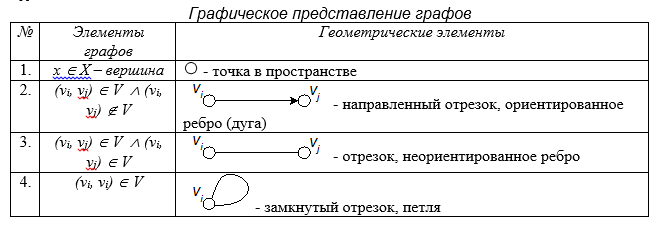
Пара (V(G), E(G)) называется простым графом, если V(G) – непустое конечное множество элементов, называемых вершинами (или узлами, или точками), а E(G) – конечное множество неупорядоченных пар различных элементов из V(G), называемых ребрами (или линиями). В простом графе данную пару вершин может соединять не более чем одно ребро.

Между элементами множества вершин и множества ребер определено отношение инцидентности. Говорят, что ребро е инцидентно вершинам v1, v2, если оно соединяет эти вершины и наоборот, каждая из вершин v1, v2 инцидентна ребру е.

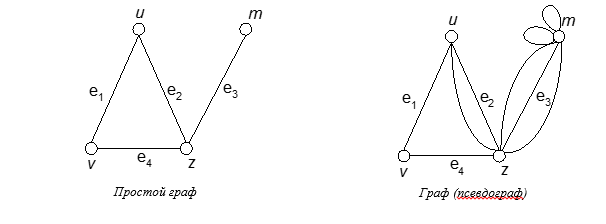
Часто бывает удобно снять ограничение, состоящее в том, что ребро должно соединять две различные вершины, и допустить существование петель.
Получающийся при этом объект, в котором могут быть и кратные ребра и петли называется графом (псевдографом).

Псевдограф без петель называется мультиграфом.

Подграфом графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Подграф называется собственным, если он отличен от самого графа.

Кратностью ребер называют количество одинаковых пар.

пример

Мультиграф в котором ни одна пара не встречается более одного раза называется графом.

Две вершины называются смежными, если существует ребро, концами которого они являются. Два ребра называются смежными, если они имеют общую вершину.

Смежные вершины – вершины, инцидентные одной дуге.
Смежные дуги – это дуги инцидентные одной вершине.

Степени вершин и полустепени исхода и захода.

Степенью вершины v графа G называется число ребер графа, которым инцидентна эта вершина.

Вершина, локальная степень которой равна 0, называется изолированной; степень которой равна 1 – висячей.

Полустепенью исхода (захода) вершины v орграфа D называется число дуг орграфа D, исходящих из вершины v (заходящих в вершину v).

Количество вершин и ребер в графе G обозначим соответственно через n(G) и m(G), а количество вершин и дуг в орграфе D – через n(D) и m(D).

Для любого псевдографа G выполняется равенство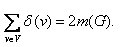

(Cумма степеней всех вершин = удвоенное количество ребер в графе)

Для любого ориентированного псевдографа D выполняется равенство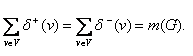

(Cумма полустепеней исхода и захода всех вершин = количество ребер в графе)

Два графа G1 и G2 называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые две вершины в G1, равно число ребер, соединяющих соответствующие вершины в G2.

Операция подразбиения (измельчения) дуги (u, v) в орграфе D = (V, E) состоит в удалении из Е дуги (u, v), добавлении к V новой вершины w и добавлении к Е | {(u, v)} двух дуг (u, w), (w, v). Аналогично определяется операция подразбиения ребра в графах.

Орграф D1 называется подразбиением орграфа D2, если орграф D1 можно получить из D2 путем последовательного применения операции подразбиения дуг. Аналогично определяется подразбиение графа.

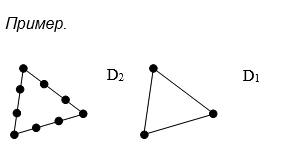
Орграфы D1, D2 называются гомеоморфными, если существуют их подразбиения, являющиеся изоморфными.

Матрицы смежностей и инциденций вершин графов и орграфов.

Матрицей смежности орграфа D называется квадратная матрица A(D)=[aij] порядка n, у которой

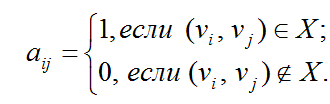
Матрицей инцидентности орграфа D называется (nxm) –матрица B(D)=[bij], у которой

Матрицей смежности графа G называется квадратная матрица A(G)=[aij] порядка n, у которой

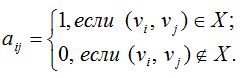
Матрицей инцидентности графа G называется (nxm) –матрица B(G)=[bij], у которой

Основные свойства матриц смежности:

Матрица смежностей вершин неориентированного графа A (G) является квадратной и симметричной относительно главной диагонали.
Элементами матрицы A (G) являются целые положительные числа и число ноль.
Сумма элементов матрицы A (G) по i-й строке (или по i-му столбцу) равна степени соответствующей вершины δ ( xi ).

Из определения следует, что сумма элементов i-й строки матрицы A (G)орграфа равна полустепени исхода δ+ ( xi ), а по i-му столбцу – полустепени захода δ¯ ( xi ).

Свойства матрицы инцидентности неориентированного графа:

Сумма элементов матрицы на i-й строке равна δ ( xi ).
Сумма элементов матрицы по i-му столбцу равна 2.

Матрица инцидентности орграфа G обладает следующими свойствами:

Сумма строк матрицы B(G) является нулевой строкой.
Любая строка матрицы B(G) является линейной комбинацией остальных строк.
Ранг матрицы B(G) равен p-1.

Основные типы графов.

Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Вполне несвязный граф обозначают Nn.

Простой граф, в котором любые две вершины смежны, называется полным. Полный граф обозначают Кn.

Граф, у которого все вершины имеют одну и ту же локальную степень n, называется регулярным (или однородным) степени n. Регулярные графы степени 3 называются кубическими (или трехвалентными). Среди регулярных графов особенно интересны так называемые платоновы графы – графы, образованные вершинами и ребрами пяти правильных многогранников - Платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.

Допустим, что множество вершин графа G можно разбить на два непересекающихся подмножества V1 и V2 так, что каждое ребро в G соединяет какую-нибудь вершину из V1 с какой-нибудь вершиной из V2, тогда данный граф называется двудольным.

Если в двудольном графе каждая вершина из V1 соединена с каждой вершиной из V2, то граф называется полным двудольным.

Граф называется связным, если его нельзя представить в виде объединения двух графов, и несвязным в противном случае.

Очевидно, что всякий несвязный граф можно представить в виде объединения конечного числа связных графов – каждый из таких связных графов называется компонентой связности графа.

Определение. Связный регулярный граф степени 2 называется циклическим графом.

Смешанный граф - Граф, содержащий как ориентированные, так и неориентированные рёбра