2. Теорема о реализуемости графов в трехмерном Евклидовом пространстве. Планарные графы. Связь между количеством вершин, ребер и граней в планарном графе (формула Эйлера).

Теорема о реализуемости графов в трехмерном Евклидовом пространстве.

Каждый конечный граф может быть реализован в трёхмерном Евклидовом пространстве
Предположим у нас есть граф имеющий м вершин и н рёбер. Тогда, выберем произвольную плоскость, и отобразим на ней точки м.
Им в соответстие поставим рёбра н, и получим модель в трхмерном евклидовом пространстве.

Планарные графы.

Укладкой графа на произвольной поверхности называется такое изображение его на этой поверхности, что ребра графа пересекаются только в его вершинах.
Сферической укладкой называется укладка графа на сфере.
Плоской укладкой называют укладку графа на плоскости.

Граф, имеющий плоскую укладку, называется плоским.
Граф, изоморфный плоскому, называется планарным.

На рис.39 (а) изображен планарный граф, (б) и (в) – две его плоские укладки.

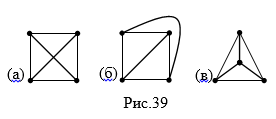
Любой простой планарный граф можно уложить на плоскости так, чтобы его ребра были прямолинейными отрезками.

Два основных непланарных графа: полный граф К5 и полный двудольный граф К3,3 называют графами Куратовского.

Теорема. Граф планарен тогда и только тогда, когда он не содержит подграфа, стягиваемого к одному из графов Куратовского.

Связь между количеством вершин, ребер и граней в планарном графе (формула Эйлера).

Укладка планарного графа на плоскости делит её на области, называемые гранями. Если грань имеет конечную площадь, назовем её конечной, иначе – бесконечной гранью. На рис.40 конечные грани – это g1, g2, g3, а g4 – бесконечная грань. Соотношение между числом вершин, ребер и граней в планарном графе было установлено Эйлером.

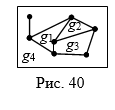
(Формула Эйлера) Если связный граф планарен и имеет v вершин, r ребер и g граней, то v – r + g = 2.

Следствие 1. Пусть G – планарный граф с v вершинами, r ребрами, g гранями и k компонентами. Тогда v – r + g = k +1

Следствие 3. Графы Куратовского K5 и K3,3 не являются планарными.

Следствие 4. В любом простом планарном графе имеется по крайней мере одна вершина степени не более 5.

Наименьшее число планарных графов, объединение которых даст граф всей сети, называется толщиной графа.

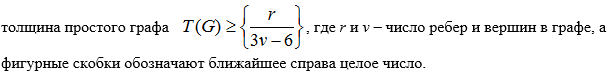
Эта оценка довольно грубая, но, тем не менее, с помощью неё часто можно получить точные результаты. Так, например, для полного графа K5 толщина, равная 2, полученная по этой оценке, является истинным значением.