21. Разбиение чисел с учетом и без учета порядка.

Рассмотрим следующую задачу: сколькими способами можно представить данное натурально число n в виде суммы: 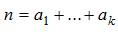, где 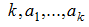– положительные целые числа.

Нетрудно заметить, что число разбиений натурального числа n на k частей, когда две суммы, различающиеся порядком слагаемых, считаются различными (такие разбиения принято называть композициями), равно числу способов, которыми можно разместить k–1 чёрточек в n–1 промежутках между n единицами, т.е. .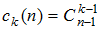

В общем случае основным методом решения задач о разбиении чисел является сведение к задаче о разбиении меньшего числа или о разбиении на меньшее число слагаемых.