4. Изоморфные графы. Алгоритм распознования изоморфизма графов.

Изоморфные графы.

Два графа G1 и G2 называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые две вершины в G1, равно число ребер, соединяющих соответствующие вершины в G2.

Из определения следует, что изоморфные графы можно одинаково изображать графически и отличаться они будут только метками вершин.

Изоморфизм графов есть отношение эквивалентности.

Алгоритм распознования изоморфизма графов.

Критерий изоморфности неориентированных графов

Неориентированные графы G и H с конечным числом вершин изоморфны тогда и только тогда, когда матрицы смежности A(G) и A(H) этих графов связаны соотношением 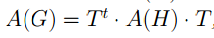, где T — подстановочная матрица, то есть матрица, в каждой строке и в каждом столбце которой имеется ровно один ненулевой элемент, равный 1.

Теорема. Для того, чтобы граф G1 был изоморфен графу G2, необходимо и достаточно выполнения следующих условий:
1. Полустепени входа и исхода соответствующих вершин равны.
2. Существует подстановка, переводящая граф G1 в граф G2.

Cформулируем алгоритм распознавания изоморфизма двух графов G1 и G2:

1. Подсчитываем число вершин каждого графа. При равенстве переходи к 2, а при неравенстве к 6.
2. Выписываем все элементы обоих графов в естественной упорядоченности и определим пары (d+(x), d-(x)) и (d+(y), d-(y)) для каждого элемента. Переход к 3.
3. Для каждого элемента x графа G1 ищем такой элемент y графа G2, что выполняется первое условие теоремы. Найденные элементы x и y соединяем ребром, т.е. строим граф соответствия. Переходим к 4. В противном случае к 6.
4. Выписываем подстановку, определяемую графом соответствия и проверяем выполнение второго условия теоремы. При выполнении условия переходим к 5. В противном случае к 6.
5. Графы изоморфны.
6. Графы не изоморфны.