5. Связные графы. Основные понятия и определения. Компонента связности. Определение компонент связности.

Граф называется связным, если его нельзя представить в виде объединения двух графов, и несвязным в противном случае.

Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Вполне несвязный граф обозначают Nn.

Очевидно, что всякий несвязный граф можно представить в виде объединения конечного числа связных графов – каждый из таких связных графов называется компонентой связности графа.

Или по-умному

Граф называется связным, если любая пара вершин связана, т.е. любые две вершины соединены цепью.

Пусть y - произвольная вершина неориентированного графа G ( X, E ). Обозначим через Xy множество всех вершин графа G, которые можно соединить с y цепями(вершину y также включаем в множество Xy). Пусть Gy — подграф графа G, множеством вершин которого является множество Xy, а множество ребер образуют все те ребра из E, концы которых принадлежат Xy. Построенный таким образом подграф Gy называется компонентой связности или связной компонентой графа G.

Ну и вот так тоже можно

Связный граф — граф, содержащий ровно одну компоненту связности. Это означает, что между любой парой вершин этого графа существует как минимум один путь.

Компонента связности графа — некоторое множество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.

Компоненты связности неориентированного графа G обладают следующими свойствами:

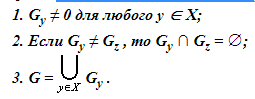
Следствие. Неориентированный граф связен тогда и только тогда, когда он состоит из одной компоненты связности.

Теорема. Неориентированный граф G = ( X, E ) связен тогда и только тогда, когда множество вершин X нельзя разбить на два непустых непересекающихся подмножества X1 и X2 , которые не соединены ни одним ребром.

Следствие. Неориентированный граф G связен тогда и только тогда, когда не существует такой нумерации вершин графа G, при которой его матрица смежности вершин имеет вид

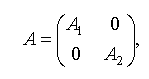
где A1 и A2 - квадратные матрицы.

Теорема. Пусть G – обыкновенный неориентированный граф с n вершинами и k компонентами связности. Тогда максимальное число ребер в графе G равно

q = 0,5( n - k )( n - k + 1 )

Следствие. Если обыкновенный неориентированный граф G с n вершинами имеет больше, чем 0,5( n - 1 )( n - 2 ) ребер, то он связен.

Определение. Орграф G ( X, E ) называется сильно связным, если для любых его вершин x и y, x ≠ y, существуют пути μ и μ’, идущие соответственно из x в y и из y в x.

Теорема. Орграф G ( X, E ) сильно связен тогда и только тогда, когда он имеет контур, проходящий через все вершины.