6. Графы – деревья. Свойства. Теорема А. Кэли. Построение минимального остовного дерева.
Графы – деревья.
Граф G называется деревом, если он является связным и не имеет циклов.
Граф G, все компоненты связности которого являются деревьями, называется лесом.
Утверждение. Если у дерева G есть, по крайней мере, одно ребро, то у него обязательно найдется висячая вершина.
Утверждение. Пусть G – дерево. Тогда любая цепь в G будет простой.
Орграф G ( X, E ) называется прадеревом или ориентированным деревом, растущим из корня x0 , при следующих условиях:
- Неориентированный граф G’, соответствующий графу G, является деревом.
- Единственная простая цепь между x0 и любой другой вершиной x графа G’ является путем в орграфе G, идущим из вершины x0 в вершину x.
Свойства.
Пусть G ( X, E ) – неориентированный граф с p вершинами и q ребрами. Тогда следующие утверждения эквивалентны:
- G есть дерево.
- Любые две различные вершины x и y графа G соединены единственной простой цепью.
- G – связный граф, утрачивающий это свойство при удалении любого из его ребер.
- G – связный граф и p = q + 1.
- G – ациклический граф и p = q + 1.
- G – ациклический граф, причем если любые две его вершины x и y соединить ребром e, то в полученном графе будет ровно один простой цикл.
В неориентированном графе G ( X, E ) вершина x называется концевой или висячей, если δ ( x ) = 1, т.е. если этой вершине инцидентно единственное ребро e. Это ребро также называется концевым или висячим. С висячими вершинами связана следующая теорема.
Теорема. В любом дереве G ( X, E ) с p ≥ 2 вершинами имеется не менее двух концевых вершин.
Теорема А. Кэли.
Помеченным деревом порядка n называется дерево, вершинам которого взаимно однозначно соответствуют числа от 1 до n.
Число помеченных деревьев с p вершинами равно 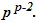 (p^(p-2))
(p^(p-2))
wiki:
Теорема Кэли о числе деревьев — названное в честь А. Кэли явное выражение в теории графов для числа деревьев с данным числом пронумерованных вершин. А именно, оказывается, что на n вершинах, пронумерованных числами от 1 до n, существует ровно n^{n-2} различных деревьев.
Построение минимального остовного дерева.
Подграф G1 ( X1 , E1 ) неориентированного графа G ( X, E ) называется каркасом или остовным деревом графа G, если G1 – дерево и X = X1.
Теорема. Граф G ( X, E ) тогда и только тогда обладает каркасом, когда он связен.
Графом c нагруженными ребрами (нагруженным графом) называется неориентированный граф G ( X, E ), каждому ребру e ∈ E которого поставлено в соответствие число μ ( e ) ≥ 0, называемое весом или длиной ребра e.
Поставим задачу нахождения такого каркаса G1 ( X1 , E1 ) в нагруженном графе G ( X, E ), для которого сумма
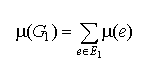
минимальна.
Каркас с таким свойством называется минимальным каркасом.
Алгоритм построения минимального каркаса.
Пусть G ( X, E ) - связный нагруженный граф с p вершинами.
Шаг 1. В качестве первого ребра искомого минимального каркаса выбираем ребро e1 с наименьшим весом μ ( e1 ). Если таких ребер несколько, то берем любое из них.
Шаг 2. В качестве второго ребра берем ребро e2 из множества E \ { e1 }, имеющее наименьший вес μ ( e2 ), и такое, что множество { e1 , e2 } не содержит простых циклов. Если таких ребер несколько, то берем любое из них.
Шаг 3. В качестве третьего ребра выбираем такое ребро e3 из множества E \ { e1 , e2 }, которое имеет наименьший вес μ ( e2 ) и для которого множество { e1 , e2 , e3 } не содержит простых циклов. Если таких ребер несколько, берем любое из них.
Указанный процесс повторяется и через некоторое число k шагов дает множество E = { e1 , e2 , … , ek }, к которому нельзя добавить ребро без появления цикла. Подграф G1 ( X, E1 ) и является минимальным каркасом графа G ( X, E ).