9. Теорема о максимальном числе ребер в графе с p вершинами и q компонентами связности.
Теорема. Пусть G – обыкновенный неориентированный граф с n вершинами и k компонентами связности. Тогда максимальное число ребер в графе G равно
q = 0,5( n - k )( n - k + 1 ).
Доказательство. Граф G имеет максимальное число ребер, если каждая компонента связности Gi , i = 1, 2, … , k имеет максимальное число ребер. Компонента связности Gi, имеющая максимальное число ребер, является полным графом. Число ребер полного графа с ni вершинами равно 0,5 · ni · ( ni - 1 ). Таким образом, максимальное число ребер графа G, компоненты связности Gi которого имеют по ni вершин, равно
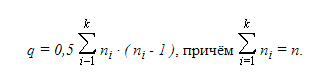
Полученное число зависит от того, как распределены вершины графа G по его компонентам связности. Предположим, что существует связные компоненты G1 и G2 графа G, имеющие более чем по одной вершине, т.е. n1 > 1 и n2 > 1. Пусть n1 ≤ n2. Рассмотрим граф Go, получаемый из графа G заменой компонент G1 и G2 на полные графы с ( n1 - 1 ) и ( n2 + 1 ) вершинами соответственно. Граф Go имеет n вершин и k компонент связности, а число его ребер равно
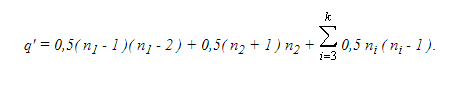
Тогда
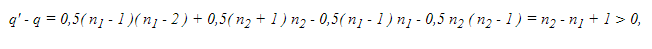
поэтому q’ > q. Итак, граф Go имеет больше ребер, чем граф G. Если и далее перестраивать граф указанным образом, то в результате получим граф, состоящий из k - 1 изолированной вершины и одной полной компоненты связности с n - k + 1 вершиной. Этот граф имеет максимальное число ребер, равное 0,5( n - k )( n - k + 1 ). Теорема доказана.
Следствие. Если обыкновенный неориентированный граф G с n вершинами имеет больше, чем 0,5( n - 1 )( n - 2 ) ребер, то он связен.
