[предыдущая тема]
[оглавление]
[следующая тема]
10. Внутренне устойчивые множества вершин.
- внутренне устойчивое (независимое) множество
- полностью зависимое множество
- максимальное внутренне устойчивое множество
- число внутренней устойчивости (плотность графа)
Определение 8.1. Пусть G(X,E) – произвольный граф. Множество вершин X1 Ì X графа G называются
внутренне устойчивыми
или независимыми, если никакие две вершины из X1 не
смежны. Множество вершин X2 Ì X графа G называется
полностью зависимым, если любые две вершины x, y Í X2 , x ¹ y смежны.
Подграф G1 графа G(X,E), порождаемый внутренне устойчивым множеством X1,
является нуль-графом. Подграф G2 обыкновенного неориентированного графа G(X,E),
порожденного полностью зависимым множеством X2, является полным графом.
Внутренне устойчивое
множество X1 графа G называется максимальным, если оно теряет свойство внутренней
устойчивости при добавлении любой вершины.
Теорема 8.1.Пусть
G(X,E) –
произвольный граф. Внутренне устойчивое множество X1 графа G является максимальным тогда и только тогда, когда
каждая вершина x Î X\X1, не имеющая петель, смежна с некоторой вершиной yÎ X1.
Доказательство.
Докажем необходимость. Предположим, что существует вершина x Î X\X1, не смежная ни с какой вершиной из X1,
причем в вершине x нет петель. Тогда множество X1 È {x} внутренне
устойчиво, вопреки максимальности X1. Итак, необходимость доказана.
Доказательство достаточности. Пусть X1
обладает тем свойством, что каждая вершина x Î X\X1, не имеющая петель, смежна с некоторой вершиной из X1. Если X1 не максимально, то существует вершина x Î X\X1, такая, что X1È{x} –
внутренне устойчивое множество. Тогда в вершине x нет петель, и вершина x не смежна ни с какой вершиной из X1.
Полученное противоречие доказывает достаточность.
Пусть E – множество всех внутренне устойчивых множеств графа G. Число
называется числом
внутренней устойчивости,
или плотностью графа G.
Метод К.Магу нахождения максимальных
внутренне устойчивых множеств
Пусть G(X,E) – ориентированный граф без параллельных ребер и X1 –
некоторое множество вершин этого графа G.
Введем булевы переменные Yi, соответствующие вершинам графа xi
(i = 1, . . . , n). Рассмотрим оценку <e1, . . . , en>
списка переменных <Y1, . . . , Yn>.
Отметим, что условие принадлежности вершины xi множеству X1 внутренне устойчивых может быть записано следующим
образом:
если eÎE
и e=<xi, xj> то xj¹X1,
а это равносильно
тому, что
для 
(8.1)
где aij – элемент
матрицы смежности вершин графа.
Условие (8.2) можно записать в виде:
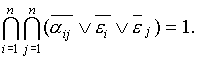(8.2)
Заметим, что при aij=0 заведомо выполняется равенство (8.1), а при aij
=1 справедливо
Поэтому условие
(8.3) можно записать так:
(8.3)
или, обозначив
в виде
(8.4)
Таким образом, справедливо следующее утверждение:
необходимым и достаточным условием внутренней устойчивости множества X1ÍX является
выполнение равенства (8.4).
Из приведенного утверждения следует, что внутренне
устойчивые множества вершин графа G, и только они, соответствуют оценкам списка переменных
<Y1, Y2, ... ,Yn), на котором выполняется равенство F = 1, что
дает простой способ выделения всех внутренне устойчивых множеств.
Для определения всех внутренне устойчивых множеств
вершин графа приведем формулу (8.4) к дизъюнктивной нормальной форме (ДНФ), а
затем, используя любой метод минимизации логических функций, к минимальной ДНФ.
Каждой элементарной конъюнкции полученного выражения соответствует множество
внутренне устойчивых вершин графа, которое содержит вершины графа, не вошедшие
в это элементарное произведение.
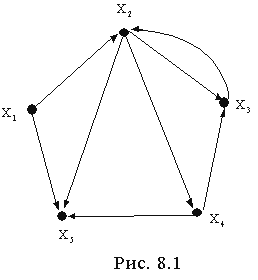
Пример 8.1. Построить множества внутренне устойчивых
вершин графа, приведенного на рис. 8.1.
Составим логическую функцию F согласно
(8.4)
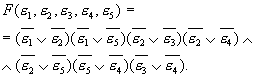
Определяем минимальную ДНФ этой функции:
Выбираем вершины, не вошедшие в состав элементарных
конъюнкций:
Нетрудно убедиться, что полученные множества являются множествами внутренне устойчивых
вершин графа, приведенного на рис. 8.1.