[предыдущая тема] [оглавление] [следующая тема]

14. Нахождение кратчайших путей в графе.

В этом параграфе рассматриваются ориентированные графы G(X, E) каждой дуге eÎE которого ставится в соответствие вещественное число l(e). Т.е. на множестве Е создана функция l:E®R. Такой граф принято называть нагруженным. Само число l называется весом дуги.

Можно увидеть аналогию между, например, картой автомобильных или железных дорог. Тогда множество вершин Х будет соответствовать городам, множество дуг – магистралям, соединяющим города, а веса – расстояниям. (На практике, при этом, фактически получится неориентированный граф).

В связи с изложенной аналогией будем называть веса дуг расстояниями.

Определение 1. Пусть имеется последовательность вершин x₀, x₁, …, x_n, которая определяет путь в нагруженном графе G(X, E); тогда длина этого пути определяется как .

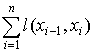Естественный интерес представляет нахождение кратчайшего пути между двумя заданными вершинами x и y.

Алгоритм Форда отыскания кратчайшего пути.

Будем предполагать, что все расстояния в графе положительны. (Если это не так, то ко всем весам можно всегда добавить такую константу, что все эти веса станут положительными).

Пусть мы ищем путь от вершины x₀ к вершине x_n. Будем каждой вершине x_i ставить в соответствие некоторое число l_i по следующим правилам.

1° Положим l₀= 0, l_i= ¥ (достаточно большое число) для "i > 0.

2° Ищем в графе дугу (x_i, x_j) удовлетворяющую следующему условию

l_j - l_i > l(x_i, x_j), (9.1)

после чего заменяем l_j на

Пункт 2°повторяется до тех пор, пока невозможно будет найти дугу, удовлетворяющую условию (1). Обоснуем этот алгоритм и укажем как определяется кратчайший путь.

Отметим, что l_n монотонно уменьшается, то после завершения алгоритма найдется дуга , такая, что для которой последний раз уменьшалось l_n. (Иначе вообще нет пути между x₀ и x_n или для верно (1)).

По этой же самой причине найдется вершина , такая , что

этот процесс может продолжаться и дальше, так что получится строго убывающая последовательность . Отсюда следует, что при некотором k мы получим .

Покажем, что – минимальный путь с длиной l_n, т.е. длина любого другого пути между x₀ и x_n не превышает k_n.

Возьмем произвольный путь и рассмотрим его длину .

После завершения алгоритма имеем следующие соотношения

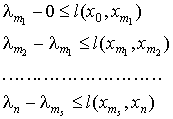
Сложив все эти неравенства, получим

что и требовалось доказать.

Рассмотрим пример.

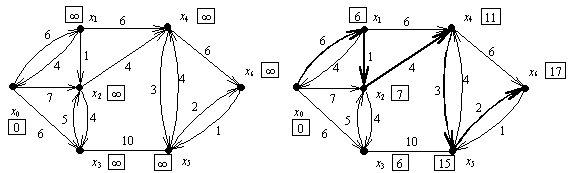а б

Рис. 10.1

На рис. 10.1а изображен исходный помеченный граф и начальные значения l_i. На рис. 10.1,б для того же графа указаны конечные значения l_i и выделен кратчайший путь. Пометка вершин графа происходила в следующем порядке (в скобках указана дуга, вдоль которой выполняется (1)):

l₁ = 6 (x₀, x₁),

l₂ = 7 (x₀, x₂),

l₃ = 6 (x₀, x₃),

l₄ = 12 (x₁, x₃),

l₄ = 11 (x₂, x₄),

l₅ = 16 (x₃, x₄),

l₅ = 15 (x₄, x₅),

l₆ = 18 (x₄, x₆),

l₆ = 17 (x₅, x₆).

Иногда возникает задача отыскания кратчайших расстояний между всеми парами вершин. Одним из способов решения этой задачи является

Алгоритм Флойда

Обозначим l_ij длину дуги (x_i, x_j), если таковой не существует примем l_ij = ¥, кроме того, положим l_ii = 0. Обозначим длину кратчайшего из путей из x_i в x_j с промежуточными вершинами из множества {x₁, …, x_m}. Тогда можно получить следующие уравнения

, (9.2)

. (9.3)

Уравнение (9.2) очевидно. Обоснуем уравнение (9.3). Рассмотрим кратчайший путь из x_i в x_j с промежуточными вершинами из множества {x₁, …, x_m, x_m₊₁}. Если этот путь не содержит x_m₊₁, то . Если же он содержит x_m₊₁, то деля путь на отрезки от x_i до x_m₊₁ и от x_m₊₁ до x_j, получаем равенство .

Уравнения (9.2) и (9.3) позволяют легко вычислить матрицу расстояний [d_ij] между всеми парами вершин графа G(X, E). На первом этапе согласно (9.2) составляем n´n матрицу равную матрице [l_ij] весов ребер (n – число вершин G(X, E)). n раз производим вычисление по итерационной формуле (9.3), после чего имеем – матрицу расстояний.

Отметим, что алгоритм Флойда непосредственно не указывает сам кратчайший путь между вершинами, а только его длину. Алгоритм Флойда можно модифицировать таким образом, чтобы можно было находить и сами пути. Для этого получим вспомогательную матрицу [R_ij], которая будет содержать наибольший номер вершины некоторого кратчайшего пути из x_i в x_j (R_ij=0, если этот путь не содержит промежуточных вершин).

Эта матрица вычисляется параллельно с по следующим правилам

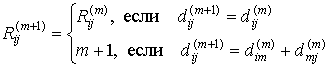
Последнее выражение следует из обоснования (9.3).

Теперь кратчайший путь выписывается из следующего рекурсивного алгоритма:

Кратчайший путь из x_i в x_j:

1°. Если R_ij = 0 то выполнить 2°,

иначе выполнить 3°.

2°. Если i=j то выписать x_i и закончить,

иначе выписать x_i и x_j закончить.

3°. Выписать кратчайший путь между x_i и .

4°. Выписать кратчайший путь между и x_j.

Пункты 3° и 4° предполагают рекурсивное обращение к рассмотренному алгоритму.

С задачей определения кратчайших путей в графе тесно связана задача транзитивного замыкания бинарного отношения.

Напомним, что бинарным отношением на множестве Х называется произвольное подмножество E Ì X ´ X.

Транзитивным называется отношение, удовлетворяющее следующему условию: если (x, y) Î E и (y, z) Î E, то (x, z) Î E для всех x, y, z Î X. Отметим, что бинарное отношение можно однозначно представить орграфом G(X, E). Теперь для произвольного отношения Е определим новое отношение Е* следующим образом

E* = {(x, y) | если в G(X, E) существует путь ненулевой длины из x в y}.

Легко проверить, что Е* - транзитивное отношение. Кроме того, Е* является наименьшим транзитивным отношением на Х в том смысле, что для произвольного транзитивного отношения F É E выполняется E* É F. Отношение Е* называется транзитивным замыканием отношения Е.

Если отношение Е представить в виде графа G(X, E) в котором каждая дуга имеет вес 1, то транзитивное замыкание Е* можно вычислить с помощью алгоритма Флойда. При этом надо учесть, что

(x_i, x_j) Î E* если .

Для большего удобства алгоритм Флойда в этом случае можно модифицировать следующим образом.

Положим

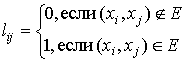Вместо (9.3) запишем

где Ú – дизъюнкция (логическое сложение),

Ù – конъюнкция (логическое умножение).

После завершения работы алгоритма будем иметь

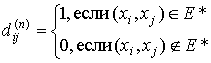
Модифицированный таким образом алгоритм называется алгоритмом Уоршелла.

[предыдущая тема] [оглавление] [следующая тема]